☰
分布定数回路
分布定数
　一般に、受動回路は、ＬＣＲの組み合わせで表すことが出来ます。これを集中定数回路と呼びます。

　しかし、伝送線路等を、それより波長が短い高周波の信号波が伝搬する時などは、 ＬＣＲの単純な組合せでは表現出来ません。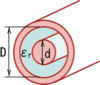
　敢えてより正しく記述するためには、(波長に比べて)微小区間のＬＣＲが分布して縦続接続されているような回路 (分布定数回路) を考えなければなりません。(上図)

　このように表現をすることで、ケーブルなどを信号波が伝搬していく様子などを表すことが出来ます。 この分布定数値の具体的な値は、外導体径Ｄ、内導体径ｄの無損失同軸ケーブルの場合、次のようになります。 　　(特性インピーダンスの計算ページ)
　Ｚo＝60／SQRT(εr)*ln(Ｄ／ｄ) ［Ω］　(特性インピーダンス)　→　50［Ω］　　　 D/d=2.3の場合
　Ｃ＝２πε／ln(Ｄ／ｄ) ［F/m］＝55.6 εr／ln(Ｄ／ｄ) ［pF/m］→　67［pF/m］　 D/d=2.3の場合
　Ｌ＝１／（Ｃ＊ｖ2） ［H/m］＝0.2 ln(Ｄ／ｄ) ［μH/m］　　 →　0.17［μH/m］ D/d=2.3の場合

　　 参考サイト：　高周波ケーブル 　同軸ケーブル 　同軸コネクタ 　特性インピーダンス
　
分布定数回路
クリックすると拡大します 　いわゆるマイクロ波でも、波長に比べて十分小さい集中定数回路で回路を組むことは可能ですが、 元々波長が短いのでそのような微細加工は現実的ではありません。

　そこで上述のような分布線路のうち、 Ｒ分の少ないＬＣの分布定数を持つ線路を組合せて、代替ＬＣ素子として回路を構成します。
　しかし、伝送線路を何百ものＬＣの縦続素子で記述することは現実的ではありません。 実際には、色々な特性インピーダンスと長さの線路小片をＬＣ素子の代わりとして組合せることで、 分布定数回路を構成します。
　なお実際のマイクロ波線路としては右図の様なものがあります。(クリックで拡大)
　
反射波
　上述のように、分布線路の中では信号波の伝搬時間を考慮しなければなりません。

　均一なケーブルの場合、ケーブル入力端に加わった時点では、ケーブルの長さも 出力端にどのような負荷が接続されているかさえも分かりませんので、その電圧が定常化されません。
　この場合、ケーブル入力端には、まず信号源電圧をその内部インピーダンスとケーブルの 「特性インピーダンス」で分圧した電圧が掛かり、その電圧が進行波として ケーブル内を出力端まで、特有の伝搬速度で進んでいきます。
　ケーブル出力端の負荷値がケーブルの特性インピーダンス値等しい時には、負荷の端子電圧となります。 この場合、「負荷はケーブルの特性インピーダンスに整合している」といいます。
　そうでない時は、ケーブル出力端では「反射」が起こり、不整合分の電圧が電源側に向かって、 反射波として戻っていきます。

　これは、一般的な波の性質と同じで、波が防波堤に当たって、跳ね返りの波が戻っていくのと似ています。 また、「波」として扱うことで、解析や理解が便利になります。 参考：波動アニメーション

　なお、電源インピーダンスと線路の特性インピーダンスが整合していない場合は、さらに反射波の反射が起こり、 再び負荷側に伝搬していくことになります。
　
反射係数
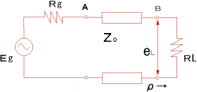
　「波動」を考えると、不連続点の振る舞いが重要なことが気付かれたかと思いますが、 分布定数回路では、その振る舞いを「反射係数」として扱います。 　反射係数を理解するために、右図のような回路を考えてみます。

　まず仮にケーブル長が零だとすると、回路は単純な集中定数回路ですから、負荷端の電圧ｅLは、

　ｅL＝ＲL／(ＲL+Ｒg)・Ｅg
　　 ＝(ＲL+Ｒg)／(ＲL+Ｒg)・Ｅg／２ ＋(ＲL-Ｒg)／(ＲL+Ｒg)・Ｅg／２
　　 ＝(１＋ρ)・Ｅg／２　　 　　ただし　ρ＝(ＲL-Ｒg)／(ＲL+Ｒg)　　：電圧反射係数

　となります。つまり、右辺の第一項目は負荷が整合しているときに負荷に加わる電圧を表し、 第二項目は負荷の不整合のために、電源側に戻る電圧を表しています。
　ここで注意しておきたいのは、負荷に最大電力が供給されるのは「整合」している場合であって、 負荷端に大きな瞬時電圧が加わることもある 「不整合」の場合ではないと言う事です。 これは波の一般的な性質でもあります。

　これに線路が加わった場合の接続点Ｂでの反射係数 ρB は、 Ｒgに変えて、線路特性インピーダンスＺoを使った次のような値になります。
　　　　ρB＝(ＲL-Ｚo)／(ＲL+Ｚo)　　：Ｂ点反射係数 　　　　　　［ ＲL／Ｚo＝(１＋ρB)／(１－ρB) ］

　Ｂ点では、この反射係数で反射された波が、電源側に戻ってゆくことになります。 ( 波動アニメを参照 )
　また接続点Ａで線路に入射する時の反射係数 ρA は、
　　　　ρA＝(Ｚo-Ｒg)／(Ｚo+Ｒg)　　：Ａ点反射係数

　となり、一旦線路特性インピーダンスＺoの負荷として線路に波が入射します。 この波は均一な線路をＢ点まで伝搬してゆき、不連続点Ｂで反射係数 ρB で反射され、 電源側に戻ってゆくことになります。
　つまり線路の入力端Ａでは、Ｂ点からの反射波がＡ点に戻ってきて、 初めて線路の先端に何が接続されていることが分かることになります。 もちろんＢ点が整合負荷(ＲL＝Ｚo)で終端されている時は、反射波が無いのでそれは分かりません。

　このように、分布定数回路では電圧の大小は物理的意味付けが軽いので、回路記述には進行波及び反射波を、 その電力を念頭においた入射波や反射波で表記することになります。
　その二端子対パラメータをＳパラメータと呼んでいます。 より詳細は、次のページで記述します。
　
リターンロス
　ここで、反射係数について、少し触れておきます。
　波動アニメで分かるように、終端側で反射が起こると、伝送線路には「定在波」が出来ます。
　上記の記述からも分かるように、その山と谷の比は、反射波が入射波に重なった場合と、反射波分下がった場合の比(次式)となり、 電圧定在波比(VSWR, Voltage Standing Wave Ratio)と呼びます。
　　　ＶＳＷＲ＝(１+|ρ|)／(１-|ρ|)
　　　ただし　ρ＝(ＺL-Ｚo)／(ＺL+Ｚo)

　また、反射係数ρは、反射電圧を表していますから、その対数値は反射電力を示すことになります。 つまり、うまく終端されないと電力が反射してくることになります。入射電力と反射電力の比をリターンロス(Return Loss）と呼んでいます。
　　　リターンロス＝-20log10(|ρ|)
　終端インピーダンスと、リターンロスおよびＶＳＷＲの関係は、右図のようになります。