Ｓパラメータ
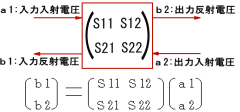反射係数の考え方を更に進め、回路の特性を、回路への入射波と反射波の関係で表す
Ｓパラメータという四端子行列表現が可能です。
分布定数回路には、何らかの形の伝送線路が結ばれますから、反射係数
のところで話をした電圧を線路の特性インピダンスの平方根で割ったものとして改めて定義しておけば、
入射波電圧を自乗すれば、それは入射波電力を表すことになるので、より便利です。
すなわち、ａi 及び ｂi は電圧を、|ａi|2 及び |ｂi|2 は電力をそれぞれ表わします。
具体的な回路の測定も、端子電圧や電流を測るのではなく、この入射波や反射波を測る
ネットワークアナライザ
を使って測定します。
スミスチャート１
～概要～
反射係数で回路特性を記述するとして、実際の回路設計をどのようにすればよいかという課題が残ります。
また回路パラメータは入射波と反射波の関係で表わされているため、測定点によりＳパラメータの値は変わってしまいます。 ただし、反射波の大きさは均一な伝送線路内では変化せず、その位相だけが変化します。
これらを考慮すると、反射波を記述する反射係数をベクトル図示し、測定点に応じてその角度を変えることで、
その表記が出来そうなことが推定されます。
更にその図表上に、その反射係数に対応したインピダンス値(若しくはアドミタンス値)をプロットしておくと、
容易に回路のインピーダンス値の表現が可能で、便利なことが予想されます。
実際、それを複素平面上に表したものが、スミスチャートと呼ばれるものです。
別の言い方をするとスミスチャートとは、反射係数 図表の上に、
インピーダンス値をプロットした図表だと言えます。
つまり、反射係数は、ρ＝(ＺL-Ｚo)／(ＺL+Ｚo) ですから、
Ｚi／Ｚo＝(１＋ρ)／(１－ρ) もしくは、 Ｙi／Ｙo＝(１－ρ)／(１＋ρ)
となり、
この各ρ に対応した正規化インピーダンスもしくはアドミタンスがプロット出来るという事です。
しかもこの両式は、ρ の代わりに－ρ を代入すると同じになりますから、ρ の代わりに－ρ を見る(180°回転)ようにすると、
インピーダンス値の代わりにアドミタンス値が分る関係になります。従って、
一つチャートがあるとインピーダンス値とアドミタンス値が同時に簡単に分る関係になります。
スミスチャート２
～性質～
スミスチャートの本質は、反射係数を複素平面上にプロットしたものですから、反射係数の性質を頭に入れて
この図表を使うと、インピーダンス値を実際の計算をせずに図表上で求めることが出来ます。
まず簡単な性質を確認しておきます。
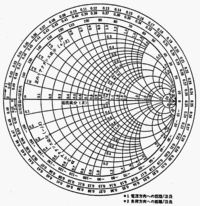
円の中心点は測定系の線路の特性インピダンスに等しい反射係数零の点です。
外周の円は反射係数の大きさが１(無損失回路)の時の色々な位相のものを表しています。
受動回路の場合は、反射係数は１以下なので、
この円の中に表現されることになります。
水平線は、純抵抗に対応し、左の端は反射係数が－１(短絡端)、
右の端は反射係数が１(開放端)に対応します。
また、水平線の上半分がインダクタンス領域、下半分がキャパシタンス領域で、
中心点の真上がリアクタンスの大きさが線路特性インピダンスに等しいインダクタンス、
真下がリアクタンスの大きさが線路特性インピダンスに等しいキャパシタンス、にそれぞれ対応します。
測定点から電源側に戻ると反射点まで距離が出来ますから、反射波は位相遅れを生じ、
その長さが半波長になると、長さ零の時と同じになり、以後それを繰り返します。すなわち、
半波長毎に反射係数ベクトルが一回転します。
左側の短絡点から電源側に４分の１波長電源側に戻ると、その点では開放線路に見えること等は図表から簡単に読み取れます。
チャートの外周には、その電気長若しくは電気角がプロットされていて、その利用を補助してくれます。
なお、インピーダンス値は、線路のインピーダンス値で正規化されて表示されており、汎用的になっています。
スミスチャート３
～利用する～
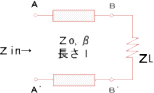左のような回路を考えて、Ｚinを求めることを考えてみます。式で表現すると、
Ｚin＝Ｚo・( ＺL＋ｊ Ｚotanβl )／( Ｚo＋ｊ ＺLtanβl ) β＝2π／λ
となります。パソコン等で計算しないとちょっと手におえない式になっています。
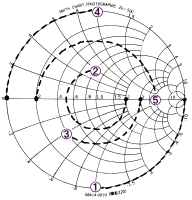
これを右図のようにスミスチャート上で考えると、簡単に変換された回路パラメータが求められます。
例えば右図の例では、
(1)は開放端から λ/8 の長さの線路を繋ぐと、正規化値１のキャパシタンスとなることを示しています。
(4)は短絡端に λ/8 の長さの線路を繋ぐと、正規化値１のインダクタンスとなることを示しています。
(5)は正規化値 0.2 の抵抗に λ/4 長さの線路を繋ぐと、正規化値５
の抵抗にインピーダンス変換できることを示します。このように伝送線路でトランスの機能も実現出来ます。
( 線路が50Ωなら10Ω→250Ω、10Ωなら2Ω→50Ωということです。
なおこの場合は先の式からも、l＝λ/4 で tanβl→∞ となるので、
Ｚin・ＺL＝Ｚo2 となり計算でも出来ます。 )
＊こちらで、色々な値を
スミスチャートにプロットしてみることが出来ます。
＊これらは、また「波形アニメーション」とを合わせてご覧になっても面白いでしょう。
回路設計
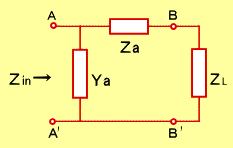マイクロ波回路の回路設計の主な課題は、インピーダンス整合です。
上で示した例を更に複雑化することで、希望する特性のインピーダンス整合回路をスミスチャート上で簡単に構成することが出来ます。
( 参照：スミスチャートでプロット )
なお、直列のインピーダンスの付加は、スミスチャート上でインピーダンス値に応じて、
図表上で足し算すれば求められます。
( 直列インピーダンスの付加 )
また、並列アドミタンスの付加は、
インピーダンスの代わりにアドミタンスをプロットした図表
( アドミタンスチャート )を用いて行います。
またこれらを組合せたイミタンスチャートを使うことで、
図表上で整合回路などが簡単に設計できます。
フィルタや発振回路の設計などもスミスチャートで検討することができます。